C번 - 카카오뷰 큐레이팅 효용성 분석 (브론즈 2) (1AC 0WA)
A번 문제를 읽고 있었는데 스코어보드에 C번에 풀리는 것을 보고 바로 C번으로 넘어왔다. 단순하게 입력을 배열에 저장하고 합을 구하는 문제였다. 첫 번째 줄 입력 받으면서 배열에 흥미도를 저장하고 전체 흥미도의 합을 구했다. 두 번째 줄 입력을 받으면서 0을 입력받은 경우 동일한 index의 흥미도를 앞서 저장한 배열에서 찾아 변수에 더했다.
알고리즘은 문제를 읽으면서 바로 파악했는데 A번 풀다가 넘어오는 시간과 C++로 구현하는 시간이 더해져 11min만에 풀었다. 더 빨리 풀 수 있었는데 늦게 제출해 조금 아쉬운 문제이다.
C번 코드
#include <iostream>
#include <algorithm>
using namespace std;
int n; // 콘텐츠의 개수
long long all_sum = 0;
long long my_view_sum = 0;
int input;
int dengrok;
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n;
int hengmis[n]; // 흥미도
for (int i = 0; i < n; i++) {
cin >> input;
hengmis[i] = input;
all_sum += input;
}
for (int i = 0; i < n; i++) {
cin >> dengrok;
if (dengrok == 0)
my_view_sum += hengmis[i];
}
cout << all_sum << "\n" << my_view_sum;
return 0;
}C번 정답 후 처음에 풀던 A번으로 다시 돌아갔다. 직관적으론 트리 각각의 노드 개수를 곱하는 문제 같은데 풀이에 확신이 들지 않았다. 계속 고민하다가 일단 보류하고 많이 풀리는 K번으로 넘어갔다.
K번 - 올바른 괄호 (골드 5) (1AC 0WA)
문제를 보자마자 하이아크 초급 알고리즘 문제셋에서 풀었던 9012 괄호 문제가 떠올랐다. 9012번은 올바른 괄호인지 아닌지만 판별하면 되지만 K번은 경우의 수까지 구해야 했다. 9012번 풀던 방식으로 계속 풀려고 하니 오히려 생각이 갇혀 잘 풀리지 않았다.
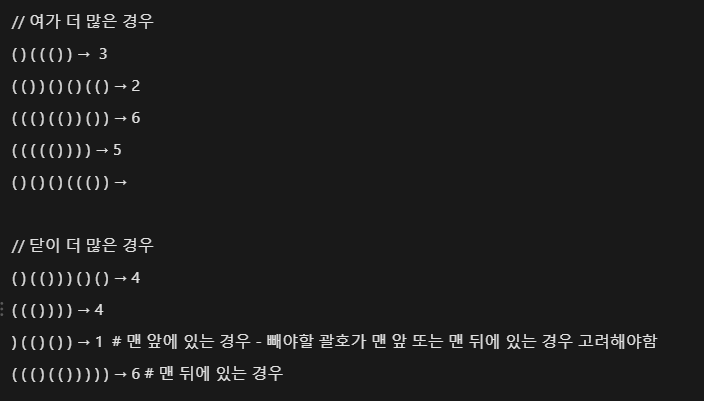
uwoobeat님과 예제를 만들어 생각해보면서 문제를 풀었다. 수많은 예제로 파악한 규칙은 열린 괄호와 닫힌 괄호의 개수 차이는 무조건 1이고, 더 많은 열린 또는 닫힌 괄호를 지워야 한다는 것이다. 입력받으면서 열린 괄호는 open, 닫힌 괄호는 close로 각각의 개수를 세고 열린 괄호가 닫힌 괄호보다 많은 경우와 그렇지 않은 경우로 나누어 풀었다.

여기서부터 uwoobeat님과 풀이가 달라졌다. 위 적힌 대로 푸셨는데 예외 케이스가 너무 많이 나왔다. uwoobeat님의 풀이를 검토하면서 예외 케이스를 하나하나 따지다 보니 부분문자열로 푸는 방법이 떠올랐다.
열린 괄호가 닫힌 괄호보다 많은 경우 앞에서부터 올바른 부분 괄호열이 만들어지면 무시하고 잘못된 괄호가 처음 나오는 위치부터 열린 괄호의 개수를 세는 방법이다.
열린 괄호가 닫힌 괄호보다 더 많다는 조건으로 앞에서부터 다시 탐색하면서 열린 괄호와 닫힌 괄호의 개수를 센다. 두 괄호의 개수가 같다면 현재 탐색한 지점까지는 올바른 부분 괄호열이므로 열린 괄호와 닫힌 괄호의 개수를 각각 0으로 초기화하고 탐색을 이어갔다. 이렇게 되면 마지막까지 탐색했을 때 올바른 부분 괄호열 이후의 어떤 위치의 열린 괄호를 지우더라도 항상 올바른 괄호가 된다.
예를 들어 ( ) ( ( ) ( ) 라고 하자. ( ) ( ( ) ( ) 를 올바른 괄호열이 될 경우는 index 2, 3, 5 에 위치한 열린 괄호 중 하나를 지웠을 때 성립한다.
0123456| open | 1 | 1 | 1 | 2 | 2 | 3 | 3 |
| close | 0 | 1 | 0 | 0 | 1 | 1 | 2 |
index 0 부터 open, close의 개수를 차례대로 센다. index 1에서 open == close이므로 현재 위치까지는 올바른 괄호열이고 open, close를 0으로 초기화한다. 이어서 끝까지 탐색하면 open == 3이 된다. open == 3은 전체 문자열에서 부분 올바른 괄호열 이후로 남은 열린 괄호의 개수가 3임을 의미한다. 따라서 올바른 괄호열을 만들 수 있는 경우의 수는 3이다.
닫힌 괄호가 열린 괄호보다 많은 경우는 입력 배열만 뒤에서부터 탐색하는 방법으로 동일한 알고리즘을 사용했다.
이렇게 K번을 풀었다. 88min에 코드를 제출하고 AC 받았다.
K번 코드
#include <iostream>
#include <algorithm>
#include <stack>
using namespace std;
string galho_string;
int open = 0, close = 0;
int more;
int more_count = 0;
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> galho_string;
int string_length = galho_string.length();
for (int i = 0; i < string_length; i++) {
if (galho_string[i] == '(')
open++;
else
close++;
}
if (open > close) {
open = 0, close = 0;
for (int i = 0; i < string_length; i++) {
if (galho_string[i] == '(')
open++;
else
close++;
if (open == close) {
open = 0, close = 0;
}
}
cout << open;
} else {
open = 0, close = 0;
for (int i = string_length - 1; i >= 0; i--) {
if (galho_string[i] == ')')
open++;
else
close++;
if (open == close) {
open = 0, close = 0;
}
}
cout << open;
}
return 0;
}A번 - 튜터-튜티 관계의 수 (실버 1) (1AC 0WA)
돌고 돌아 다시 A번으로 돌아왔다. 앞서 직관적으로 생각했던 트리 각각의 노드 개수를 곱한다를 검증하기 위해 차근차근 따져보았다.
친분 관계 그래프는 독립적인 여러 개의 트리로 이루어져 있다. 그래서 각각의 트리를 따로 생각해야 한다.
하나의 트리는 사이클이 없는 양방향 그래프이다. 따라서 하나의 트리에선 어떤 노드를 선택하더라도 전체 탐색을 할 수 있다. 여기서 전체 탐색을 할 수 있다는 것은 모든 교육생에게 교육 자료를 전달할 수 있다는 것이다.
그리고 탐색을 시작할 노드가 정해지면 튜터가 튜티에게만 전달할 수 있다는 규칙에 의해 탐색 경우의 수는 하나로 고정된다.
따라서 트리를 탐색하는 경우의 수는 트리의 전체 노드 개수가 된다.
정리하면 친분 관계 그래프는 독립적인 여러 개의 트리로 이루어져 있고, 하나의 트리를 탐색하는 경우의 수는 트리의 전체 노드 개수이다. 즉, 친분 관계 그래프를 탐색하는 경우의 수는 트리 각각의 전체 노드 개수의 곱이다.
예를 들어 친분 관계 그래프가 노드 개수가 3인 트리와 4인 트리로 이루어져 있다고 할 때 그래프 탐색 경우의 수는 12이다. (3 X 4 = 12)
트리의 개수를 구하고 각 트리의 전체 노드 개수를 구하는 알고리즘은 DFS를 이용했다.
노드를 하나씩 탐색하면서 아직 방문하지 않는 노드라면 방문 처리하고 전체 노드의 개수 count_node에 1을 더해 노드의 개수를 센다. 하나의 트리 탐색을 끝내고 나면 result에 전체 노드의 개수 count_node를 곱한다.
이렇게 해서 144min에 A번을 풀었다. 연습 때 DP랑 DFS를 중점적으로 공부했었는데 DFS로 푸는 문제가 나와서 기분이 좋았다.
A번 코드
#include <iostream>
#include <algorithm>
#include <stack>
#include <vector>
#include <set>
using namespace std;
int n, m; // 노드 개수 , 간선 개수
int u, v;
int count_node = 0;
long long result = 1;
set<int> nodes;
vector<int> graph[200001];
bool is_visited[200001] = { false };
void DFS(int node) {
is_visited[node] = true;
count_node++;
for (auto next : graph[node]) {
if (is_visited[next] == false) {
DFS(next);
}
}
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
for(int i = 0 ; i < m; i++) {
cin >> u >> v;
graph[u].push_back(v);
graph[v].push_back(u);
nodes.insert(u);
nodes.insert(v);
}
for (auto node: nodes) {
if (is_visited[node] == false) {
DFS(node);
if (count_node != 0)
result = (result * count_node) % 1000000007;
count_node = 0;
}
}
cout << result << "\n";
return 0;
}L번 - 팰린드롬 게임 (골드 4) (1AC 0WA)
L번은 wltnjeon0119님이 혼자서 푸시다가 다 같이 달라붙어서 푼 문제이다.
먼저 풀던 wltnjeon0119님이 베스킨라빈스31 게임 같은 문제라고 알려주셨다. 베스킨라빈스31 게임의 필승 조건은 본인과 상대방이 부르는 숫자의 개수 합을 4개로 일정하게 맞추는 것이다.
L번도 필승 조건을 찾아야 했다. 하지만 문제를 뚫어져라 봐도 필승 조건을 알 수 없어서 1부터 2, 3, 4, 5... 모든 테스트 케이스를 일일이 구해보았다. 처음에는 테스트 케이스를 잘 못 구해서 이상한 수열이 나왔다. 19, 23에서 갑자기 1이 튀어나오고 규칙이 전혀 보이지 않았다.
다들 반쯤 넋이 나가 있을 때쯤 스코어보드에 불코도의 다른 팀인 ‘우승못하면전학감’팀이 L번을 맞춘 걸 확인했다. 저 팀이 풀었다면 우리도 구할 수 있는 규칙일 것이라고 판단하여 1부터 다시 따져보기 시작했다.

다시 구한 결과, 1~9 는 0, 10은 1, 11 ~ 19는 0, 20은 1, 21 ~ 29는 0, 30은 1...이라는 예쁜 수열을 얻게 되었다. 10의 배수이면 필승한다는 규칙이었다. 사실 30 이후로는 따져보지 않았지만, 테스트케이스를 구하면서 1부터 9까지는 무조건 팰린드롬 수이기 때문에 10의 배수를 만들어버리면 무조건 이긴다는 것을 알게 되었다.
uwoobeat님이 규칙을 확인하려고 100 이상의 테스트 케이스도 확인해보자고 했다. 100 이상을 구하기엔 시간도 오래 걸리기도 하고 약간의 꼼수(?)를 부려 다른 팀들이 한 번에 AC를 받는 걸 보고 특이 케이스가 없겠다고 생각했다.
그래서 더 검증하지 않고 코드를 완성했다. wltnjeon0119님이 python으로 코드를 작성해주셨고 바로 제출해서 196min 만에 AC를 받았다.
L번 코드
import sys
input = sys.stdin.readline
pair = lambda : map(int, input().split())
tesc = int(input())
for i in range(tesc):
tmp = int(input())
if tmp % 10==0:
print('1')
else:
print('0')'[기록]' 카테고리의 다른 글
| [기록] 2022년 회고 - 컴공 2학년 (13) | 2023.01.03 |
|---|---|
| [기록] 2022 요약 (3) | 2023.01.01 |
| SUAPC 2022 Winter 참가 후기 (0) | 2022.04.27 |
| HI-ARC 하이아크 운영진 면접 후기 (0) | 2022.04.27 |
| 멋쟁이사자처럼 홍익대 10기 지원서 + 면접 질문 (4) | 2022.04.20 |